Г е к с а м и н о
+2
Admin
Арина
Участников: 6
Страница 1 из 5
Страница 1 из 5 • 1, 2, 3, 4, 5 
 Г е к с а м и н о
Г е к с а м и н о
Сегодня Админ предложил нам новую математическую загадку - Гексамино.
https://prarod.forum2x2.ru/t2p33-topic#15070
По видимости фигуры гексамино как-то соотносятся с Рунами Рода.
Перенесу из Википедии.
http://ru.wikipedia.org/wiki/%C3%E5%EA%F1%E0%EC%E8%ED%EE
Классификация гексамино по симметрии

35 свободных фигур гексамино по их свойствам симметрии можно разделить на 5 категорий:
Для односторонних гексамино (то есть если зеркальные отражения фигур считать различными), первая и четвёртая категории удваиваются в численности, что даёт дополнительно 25 гексамино, то есть в общей сложности 60. Для фиксированных гексамино (то есть если повороты также рассматривать как различные фигуры), то первая категория возрастёт в восемь раз по сравнению со свободнми гексамино, следующие три категории — в четыре раза, а из последней категории — в два. Это даст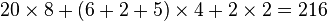 фиксированных гексамино.
фиксированных гексамино.
Составление фигур из гексамино
[ltr][править | править исходный текст][/ltr]


Квадрат 15×15 с отверстием 3×5, составленный из гексамино
Хотя полный набор из 35 гексамино имеет общую площадь 210 квадратов, из них невозможно составить какой-либо прямоугольник с такой площадью (3×70, 5×42, 6×35, 7×30, 10×21, 14×15) — в отличие от 12 пентамино, из которых можно сложить любой из прямоугольников 3×20, 4×15, 5×12 и 6×10. Доказать это можно, раскрасив гексамино и прямоугольник в шахматном порядке. Тогда 11 фигур гексамино будут иметь чётное количество квадратов обоих цветов (2 белых и 4 чёрных или наоборот), а остальные 24 гексамино — нечётное (3 белых и 3 чёрных). Таким образом, в любой фигуре, составленной из полного набора гексамино, число квадратов каждого цвета будет чётным. Но любой прямоугольник из 210 квадратов будет иметь 105 чёрных квадратов и 105 белых, то есть нечётное число.
Тем не менее, есть другие симметричные фигуры из 210 квадратов, которые могут быть составлены из гексамино. Например, квадрат 15×15 с прямоугольным отверстием 3×5 в центре имеет 106 белых и 104 чёрных квадрата (или наоборот) и может быть составлен из полного набора в 35 гексамино[2].
Некоторые симметричные укладки гексамино
[ltr][править | править исходный текст][/ltr]
Кроме того, из 60 односторонних гексамино, имеющих общую площадь в 360 единичных квадратов, можно составить прямоугольники 5×72, 6×60, 8×45, 9×40, 10×36, 12×30, 15×24 и 18×20[3].
Развёртки куба
[ltr][править | править исходный текст][/ltr]

11 из 35 фигур гексамино являются развёртками куба (см. рисунок)[4]. Сложить из них прямоугольник площадью в 66 единичных квадратов невозможно[5].
И вот ещё статья интересная http://stepanov.lk.net/gardner/hex/hex13.html
https://prarod.forum2x2.ru/t2p33-topic#15070
По видимости фигуры гексамино как-то соотносятся с Рунами Рода.
Перенесу из Википедии.
http://ru.wikipedia.org/wiki/%C3%E5%EA%F1%E0%EC%E8%ED%EE
Классификация гексамино по симметрии

35 свободных фигур гексамино по их свойствам симметрии можно разделить на 5 категорий:
- 20 фигур гексамино (на рисунке изображены серым цветом) асимметричны;
- 6 гексамино (изображены красным) имеют ось симметрии, параллельную линиям квадратной сетки;
- 2 гексамино (изображены зелёным) имеют диагональную ось симметрии;
- 5 гексамино (изображены синим) имеют центральную (вращательную) симметрию второго порядка;
- 2 гексамино (изображены фиолетовым) имеют две оси симметрии, параллельных линиям сетки.
Для односторонних гексамино (то есть если зеркальные отражения фигур считать различными), первая и четвёртая категории удваиваются в численности, что даёт дополнительно 25 гексамино, то есть в общей сложности 60. Для фиксированных гексамино (то есть если повороты также рассматривать как различные фигуры), то первая категория возрастёт в восемь раз по сравнению со свободнми гексамино, следующие три категории — в четыре раза, а из последней категории — в два. Это даст
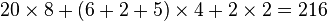 фиксированных гексамино.
фиксированных гексамино.Составление фигур из гексамино
[ltr][править | править исходный текст][/ltr]


Квадрат 15×15 с отверстием 3×5, составленный из гексамино
Хотя полный набор из 35 гексамино имеет общую площадь 210 квадратов, из них невозможно составить какой-либо прямоугольник с такой площадью (3×70, 5×42, 6×35, 7×30, 10×21, 14×15) — в отличие от 12 пентамино, из которых можно сложить любой из прямоугольников 3×20, 4×15, 5×12 и 6×10. Доказать это можно, раскрасив гексамино и прямоугольник в шахматном порядке. Тогда 11 фигур гексамино будут иметь чётное количество квадратов обоих цветов (2 белых и 4 чёрных или наоборот), а остальные 24 гексамино — нечётное (3 белых и 3 чёрных). Таким образом, в любой фигуре, составленной из полного набора гексамино, число квадратов каждого цвета будет чётным. Но любой прямоугольник из 210 квадратов будет иметь 105 чёрных квадратов и 105 белых, то есть нечётное число.
Тем не менее, есть другие симметричные фигуры из 210 квадратов, которые могут быть составлены из гексамино. Например, квадрат 15×15 с прямоугольным отверстием 3×5 в центре имеет 106 белых и 104 чёрных квадрата (или наоборот) и может быть составлен из полного набора в 35 гексамино[2].
Некоторые симметричные укладки гексамино
[ltr][править | править исходный текст][/ltr]
- «Параллелограмм» 15×14 с зубчатыми боковыми сторонами

- Прямоугольник 19×11 с одноклеточным выступом

- Прямоугольник 13×16 с двумя выступами

- «Треугольник» с зубчатой гипотенузой

- Прямоугольник 17×15 с крестообразным отверстием

Кроме того, из 60 односторонних гексамино, имеющих общую площадь в 360 единичных квадратов, можно составить прямоугольники 5×72, 6×60, 8×45, 9×40, 10×36, 12×30, 15×24 и 18×20[3].
Развёртки куба
[ltr][править | править исходный текст][/ltr]

11 из 35 фигур гексамино являются развёртками куба (см. рисунок)[4]. Сложить из них прямоугольник площадью в 66 единичных квадратов невозможно[5].
И вот ещё статья интересная http://stepanov.lk.net/gardner/hex/hex13.html
Последний раз редактировалось: Арина (Ср Мар 16, 2022 3:53 pm), всего редактировалось 5 раз(а)
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
а ещё там в рисунок закралась ошибка - одна фигурка не из шести квадратиков


\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Ой, они даже по отделам позвоночника разделены)) Осталось понять - как соотносятся с резами.
И 1 и 2 тоже отделены.
Надо наверное понять логику размещения цветов и ответвлений...
И 1 и 2 тоже отделены.
Надо наверное понять логику размещения цветов и ответвлений...
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Последний раз редактировалось: Арина (Ср Мар 16, 2022 4:32 pm), всего редактировалось 2 раз(а)
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Последний раз редактировалось: Арина (Ср Мар 16, 2022 4:31 pm), всего редактировалось 2 раз(а)
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Последний раз редактировалось: Арина (Ср Мар 16, 2022 4:29 pm), всего редактировалось 2 раз(а)
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о

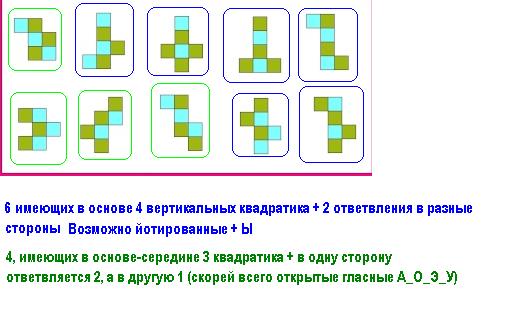
Если взять по числам, то из семи шейных рун как раз четыре имеют в сомножителях две двойки (12,18,20,28). И здесь в 4-х вариантах к основе из трёх квадратов крепится слитное добавление из 3-х квадратов.
Руну Р выделяем сразу. А в оставшихся двух к основе из трёх квадратов добавляются 1+2 по отдельности. Это руны 18 и 30, имеющие в сомножителях (2*3).

Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Для грудного отдела доп. квадратики всегда приставлены с одной стороны, в поясничном - всегда с двух сторон.
В других отделах это не работает, там нет прямых линий длиннее трёх квадратов, и получаются более сложные загогулины.
В других отделах это не работает, там нет прямых линий длиннее трёх квадратов, и получаются более сложные загогулины.

Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Елена пишет:Для грудного отдела доп. квадратики всегда приставлены с одной стороны, в поясничном - всегда с двух сторон.
В других отделах это не работает, там нет прямых линий длиннее трёх квадратов, и получаются более сложные загогулины.
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Лен, а во втором ряду второй почему? Если основу брать цельную вертикаль - то там один вправо, два влево?Елена пишет:
Если взять по числам, то из семи шейных рун как раз четыре имеют в сомножителях две двойки (12,18,20,28). И здесь в 4-х вариантах к основе из трёх квадратов крепится слитное добавление из 3-х квадратов.
Руну Р выделяем сразу. А в оставшихся двух к основе из трёх квадратов добавляются 1+2 по отдельности. Это руны 18 и 30, имеющие в сомножителях (2*3).
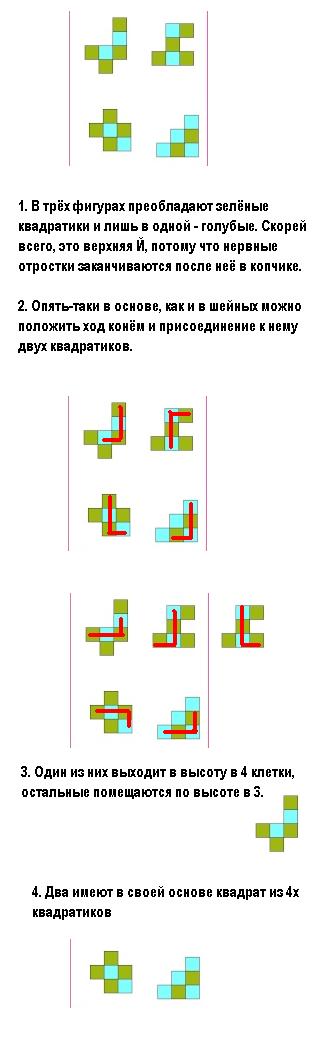
Тут ещё ход конём в них просматривается. Буквой Г, может его как-то учитывать?
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Арина пишет:Лен, а во втором ряду второй почему? Если основу брать цельную вертикаль - то там один вправо, два влево?Елена пишет:
Если взять по числам, то из семи шейных рун как раз четыре имеют в сомножителях две двойки (12,18,20,28). И здесь в 4-х вариантах к основе из трёх квадратов крепится слитное добавление из 3-х квадратов.
Руну Р выделяем сразу. А в оставшихся двух к основе из трёх квадратов добавляются 1+2 по отдельности. Это руны 18 и 30, имеющие в сомножителях (2*3).
Да, верно))

Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Последний раз редактировалось: Арина (Ср Мар 16, 2022 4:34 pm), всего редактировалось 3 раз(а)
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Копчик как-то так складывается:



Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
А можно здесь напрямую соотнести топологию квадрат и топологию треугольник? Чтобы руны эти увидеть.Арина пишет:Сегодня Админ предложил нам новую математическую загадку - Гексамино.
https://prarod.forum2x2.ru/t2p33-topic#15070
По видимости фигуры гексамино как-то соотносятся с Рунами Рода.
У нас где-то была такая тема про виды рун в разных топологиях.

Runes- Дата регистрации : 2010-02-28
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Runes пишет:
А можно здесь напрямую соотнести топологию квадрат и топологию треугольник? Чтобы руны эти увидеть.
У нас где-то была такая тема про виды рун в разных топологиях.
Не, Тань топологии напрямую здесь не видно.
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
А вот так разместились 11 развёрсток куба, представленных в Гексамино. 8 из них проявились в зоне гласных, оставив лишь две модельки незадействованными (возможно это и есть Ы и И, а не те, что я предполагала здесь https://prarod.forum2x2.ru/t1085-topic#15076), а 3 - в зоне шейных, одна из которых принадлежит предполагаемому Р.
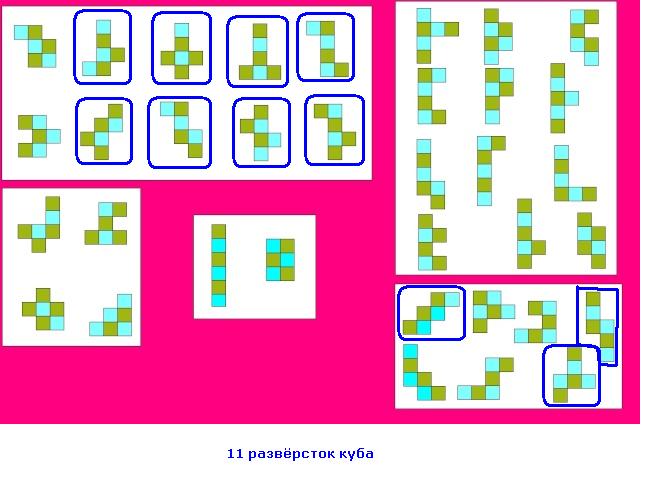

Последний раз редактировалось: Арина (Ср Мар 16, 2022 4:07 pm), всего редактировалось 1 раз(а)
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Я думаю она есть, только смотреть надо знать что, возможно углы это или как бусины закономерность в цветах. Хочется проверить во всяком случае)Арина пишет:Runes пишет:
А можно здесь напрямую соотнести топологию квадрат и топологию треугольник? Чтобы руны эти увидеть.
У нас где-то была такая тема про виды рун в разных топологиях.
Не, Тань топологии напрямую здесь не видно.

Runes- Дата регистрации : 2010-02-28
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Посмотрим дальше стандартную классификацию: куда в модели Админа выпадают чётность (2+4) и нечётность (3+3) в цветах квадратиков.
И Опять у нас пояснично-крестцовый отдел выделился)) там к его 8 свёрткам куба добавляется то, что 4 из них чётные, а 4 нечётные. Будет ли это делением на открытые-йотированные гласные?
Копчик - все четыре руны чётные. И ещё присутствуют 3 чётных в грудном отделе.
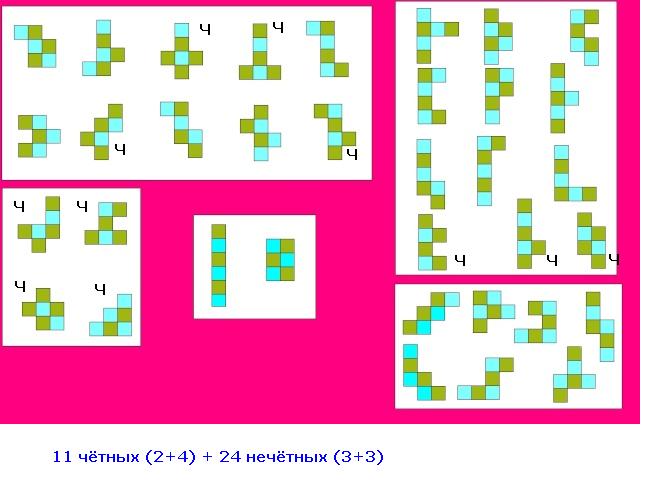
Вообще снова повторяется число 11 ну и конечно же 24.
То есть
11 чётных - 24 нечётных
11 развёрток куба - 24 неразвёрток куба
Понять бы - что же касается "башенок"?
В статье - это построение максимально высокой симметричной фигуры.
И Опять у нас пояснично-крестцовый отдел выделился)) там к его 8 свёрткам куба добавляется то, что 4 из них чётные, а 4 нечётные. Будет ли это делением на открытые-йотированные гласные?
Копчик - все четыре руны чётные. И ещё присутствуют 3 чётных в грудном отделе.

Вообще снова повторяется число 11 ну и конечно же 24.
То есть
11 чётных - 24 нечётных
11 развёрток куба - 24 неразвёрток куба
Понять бы - что же касается "башенок"?
В статье - это построение максимально высокой симметричной фигуры.
Последний раз редактировалось: Арина (Ср Мар 16, 2022 4:12 pm), всего редактировалось 1 раз(а)
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Сама единая башенка? Да, я думала про это. Просто надо как-то видимо из каждого отдела выстроить свой этаж?
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Из приведённых в статье примеров только одна башенка из Гексамино -
из 11 развёрсток куба, то есть из 8 гласных и 3х шейных

из 11 развёрсток куба, то есть из 8 гласных и 3х шейных

\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Арина пишет:Сама единая башенка? Да, я думала про это. Просто надо как-то видимо из каждого отдела выстроить свой этаж?
Ну да))
На самом деле вопрос ещё и в том, а можно ли допускать при складывании внутри отделов дырки?

Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Без дырок вряд ли башенку соберёшь. Важно чтоб симметричность была видимо. И возможно надо учитывать шахматный порядок.
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/

Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о

Шейный отдел - самый приличный вариант.

Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Поясничный отдел. Пока так...



Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
то есть полная симметричность всё-таки не выходит? Попробую тоже сегодня организовать себя...
\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Арина пишет:то есть полная симметричность всё-таки не выходит?
Думать надо, пробовать...
Просто выкладываю, чтобы потом использовать подходящие кусочки))

Елена- Географическое положение : Ростов-на-Дону
Дата регистрации : 2008-09-19
Настроение : Да будет Свет!
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
Лен, насчёт копчика согласна - самая симметричная фигура получается квадрат без одного квадратика, составляющаяся вот таким путём


ну и просто так..
есть вот такая красивая фигурка из двух деталек

к ней если присоединить недостающее получится почти симметричная фигурка, если бы один крайний правый зелёный квадратик вниз переместить))

а если учитывать шахматную последовательность, то наиболее гармоничной мне показалась вот такая выкладка прямоугольником



ну и просто так..
есть вот такая красивая фигурка из двух деталек

к ней если присоединить недостающее получится почти симметричная фигурка, если бы один крайний правый зелёный квадратик вниз переместить))

а если учитывать шахматную последовательность, то наиболее гармоничной мне показалась вот такая выкладка прямоугольником

\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/\/
фотохостинг https://postimages.org/
 Re: Г е к с а м и н о
Re: Г е к с а м и н о
А могут ли при встрече накладываться одинаковые квадраты друг на друга? также как двойные резы к примеру теоретически?

Runes- Дата регистрации : 2010-02-28
Страница 1 из 5 • 1, 2, 3, 4, 5 
Страница 1 из 5
Права доступа к этому форуму:
Вы не можете отвечать на сообщения|
|
|






» Артефакты и исторические памятники
» Эту загадку решал Шива
» Слог КН (сворачивается к Ю)
» Цвет и его проявления.
» Просто интересно...
» Заметки, ссылки, статьи и прочее.
» Поиск 31 вечной группы через работу с вечными слогами
» Слог ЗМ (сворачивается к Ю)